In this activity, students will build their first "factor trees". They will practice organizing information, identifying the commutative property, and discovering strategies to help ensure they have identified all the possible factors.

Begin by modeling how to factor systematically. We recommend starting with 24 as students have seen this value previously and are familiar with it. Some numbers, like 36, will present challenges that will be covered in a later lesson. If picking an alternative value, ensure all factors (except the number itself) are no larger than 10.

Show students the following image and explain we call this a factor tree.

Our goal is to find all the ways to build 24 with different block sizes without missing any possibilities. Allow students to guide the completion of the tree.

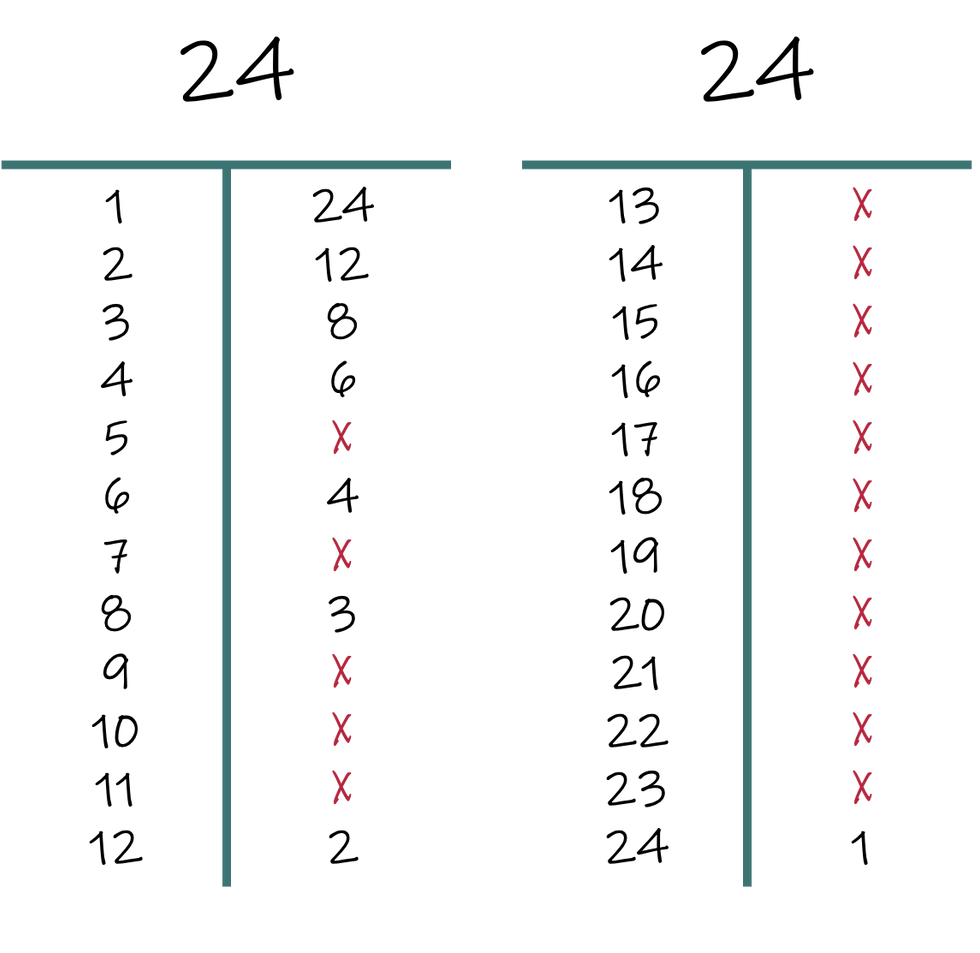
Begin by transcribing a 1 on the left. Ask students how many 1-blocks are needed to build a 24? Once students have determined 24 blocks are needed, transcribe the 24 in the right column in the same row as the 1.

Explain we will count by ones to ensure we do not miss any possibilities. Under the 1 in the left column, write down 2 and ask students how many 2 blocks we need. Remind students they can count by twos up to 24 to determine how many. If needed, students may use their fingers, or write tallies, to keep track as 12 is outside our multiplication table. Students should determine we will need 12 two-blocks to make 24.

Continue in this fashion with 3 and 4. Students can skip count as needed to complete the grid.

The next value is 5. Allow students to decide if they can create 24 using 5-blocks. Ask students to explain their reasoning. Some ideas are: we cannot reach 24 by skip counting by fives as we would have 20 and then 25 and 24 is skipped, or, all multiples of 5 have a 5 or a 0 in the one's place, as adding five makes another ten for every other sum. Write 5 on the left and mark an X on the right. When students develop this skill, they will no longer need to write every value, but for now, encourage students to write each number to ensure they do not miss anything.

Proceed in filling out the tree up to 24. This is important to allow students to discover a better way, rather than giving them a better way. We broke our tree into two parts to conserve space.

If possible, allow students a few minutes in small groups to discuss what they notice and what they wonder. Allow students to share and make a list of their ideas. Here are a few good ones to highlight:

• Twelve is splitting the 24 into two groups. No number larger than 12 can make 24 except for 24. Will this always happen? (Yes! For an even number, any value larger than half won't work as half is made up of two-blocks and the only thing smaller than 2 is 1. For an odd number, we can jump to a close even number - for instance, with 21 we could jump to 20 - and find the same result).

• If we think about our previous activity, Block Target, many of the rectangles made were rectangles we already had but tipped over. This is the commutative property. We see 2 and 12 as well as 12 and 2 on the table.

• After 4 on the left, all the numbers on the right are numbers we already have on the left.

Before solidifying a factoring strategy, allow students to play independently to pick up on patterns. Launch Block Target Play with the following settings:

• Timer: off

• Hints: off

• Count Reflections: off

If your student is in need of additional support you can allow Hints to be on.

Encourage students to work on a systematic approach to finding all the factors. As they play, have students write down their factor trees. If your students need more direction, advise them to begin by placing the vertical slider on the left at 1, create the target rectangle, and write down the pair before moving the vertical slider to 2, 3, 4, and so on, increasing the slider by one each time.

Conclude the activity with a discussion. Ask students to share their strategies and their findings. Note, it is likely that students came across difficult values. For instance, a student may recognize that 36 is even and thus can be reached by counting by twos, but is not sure how to find how many twos easily. For now, encourage skip counting. In a subsequent lesson, we will find an amazing and magical way to discover these factors as well!