Napier's Bones is a powerful tool for introducing multi-digit multiplication, fostering an understanding of place value, and improving student fluency with multiples.

You'll need a set of bones to practice. We provide step-by-step instructions on how to make your own set of bones as well as a downloadable set of bones and our Digital Bones for easy play from anywhere!

• Make Your Own Bones

• MathBait™ Digital Bones

Once you have your own set of bones, it's time to play with them and create some serious math magic. You might be surprised with how quickly and easily you can multiply large values. Grab your bones or open our digital game in a new window to practice along with the steps.

Step 1: Collect Your Bones

The first step in multiplying is to collect the bones you need. You'll find it's easiest to collect the bones for the larger value. For instance, if multiplying 1967×8, we'll collect the 1, 6, 7, and 9 bones.

Next, line up your bones up to create the number you wish to multiply. Since we are multiplying 1967 we will arrange our bones in this order.

Step 2: The Lead Bone

Place your lead bone to the left and line it up with the bones you have collected. We need to determine what row to focus on. If multiplying a multi-digit number, start with the largest place value. For instance, if multiplying 1967×58, we would focus on the 5th row first. Since we are multiplying 1967×8, we'll focus on the 8th row.

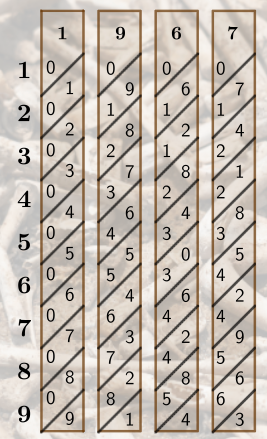
Set 3: Sum the Joints

The design of the bones create "joints". The first and last are always triangles, while the middle joints form parallelograms. For 1967×8, our first joint is a 6, so we transcribe this value. The next joint shows us an 8 and a 5. Since 8+5=13, we transcribe a 3 and carry a 1 over to the next joint.

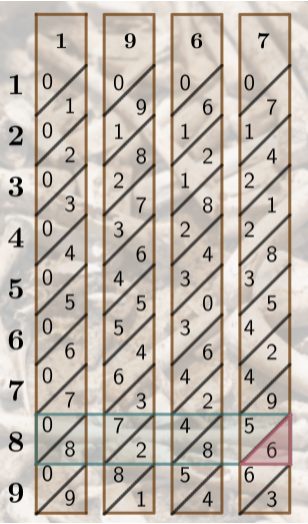
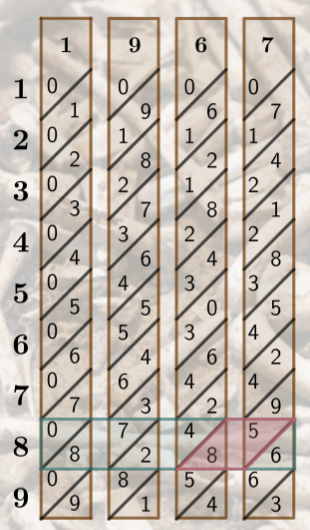
Next, we have 2 and 4. Adding the values gives us 6, plus the 1 from the previous joint gives us 7. So far we have 763 transcribed. The penultimate joint shows us 8+7=15, again we transcribe the 5 and carry the 1 over to the final joint and end up with 15736. This is the value of 1967×8.

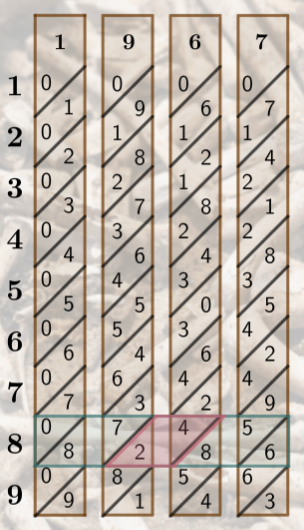
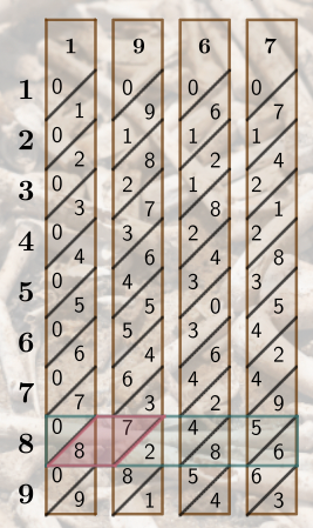
We selected a more complex example to cover all cases, however, there are many multiplication problems students can complete by simply looking at a set of bones. For instance, 7512×6 can be found to be 45,072 with just a glance! You got this.

To practice, try out our digital bones. This highlights each joint (as in the images above) and provides carrying and addition support. This is a great way to help students become familiar with using the bones.

Multiplying Larger Values

What about 1967×58, or even larger values? Place value plays a huge role in multiplying larger values. Just as we did above, we would reference the 8th row, but we would also need to reference and transcribe the value from the 5th row.

Noting that multiplying by 58 is really multiplying by 50+8, we must place our transcribed value for the 5th row into the tens place. To find the final product we then simply add our two transcribed values. Let's look at an example with 436×82.

Unlike the standard algorithm, Napier begins with the largest digit. After we collect our 4, 3, and 6 bones and align them with our lead bone, we will first focus on the 8th row.

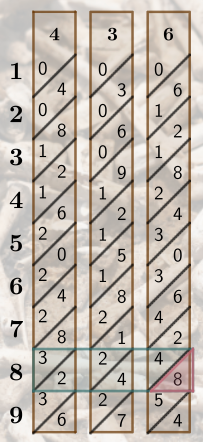
This has no carrying. From simply looking at the bones we see that 436×8=3488. As our goal was to multiply 436×82, we must note that we were interested in multiplying 436×80 rather than 436×8. Thus, we must transcribe 3488×10=34880.

Next, we shift our focus to the second row in order to multiply 436×2.

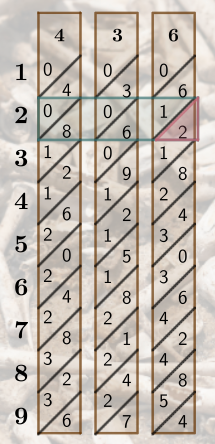
Again, we can see the value quite easily, 436×2=872. 

To complete our product, we must sum both values. Notice how this process is simply applying the Distributive Property that students were introduced to in MathBait™ Multiplication Part 3! This exercise is great practice for both addition of large numbers and using the distributive property.

So what is 436×82? Summing our transcribed values of 34880 and 872 we find

436×82=35752.

The larger the factors, the more values to sum. Thus, Napier's Bones can require some pen and pencil work. Our digital bones includes an addition helper to keep track of place value and carrying allowing young students to find products with ease.