Vedic mathematics is a system of computation discovered by Indian mathematician Tirthaji. The word Veda derives from the Sanskrit for "knowledge". A benefit of Vedic mathematics is that it is said to decrease the speed of calculations. However, this also brings about the problem with this form of math: it does not rely on understanding.

The first volume on this method was written in 1957. Students being taught at this time certainly needed a quick way to compute. Today, if a computation must be done quickly, we have calculators, phones, computers, and tablets that can handle this much better than a human ever could. This makes Vedic mathematics less useful now than at the time of its conception.

However, we should not discount Tirthaji's work; it is in fact exactly what MathBait™ encourages from its students. He looked at a problem and asked "is there an easier way?". In order develop new methods that could be taught to millions, he had to possess a deep understanding of what mathematics was. How amazing! This is our goal. We work to help our students develop a deep conceptual understanding so they can create and discover their own methods and strategies. With this strong foundation, there is no limit on what they are able to do.

Let's take a look at the Vedic method of multiplication. If you have read the previous sections, you probably won't be surprised to know it is all the same, the only difference is the viewpoint.

Step 1: Write the Product Vertically

To fully understand this method, we will use an example of 1362×298. We start by writing the product vertically, however, for this method it can be helpful to leave a bit of space between the factors.

As with other methods, we begin by multiplying the ones place and transcribing the result below the line. In this case we have a value larger than 9, and yes, we still have to carry! Rather than place the value atop the first factor, we place the tens digit below and one place to the left.

Next, we multiply in the form of a cross and sum the results. Again, we place the ones digit on the first line and any value carried below and to the left.

For our next digit we must form a star. Again, we find each product and the sum, transcribe the ones digit on the first line and any value carried below and to the left.

Our next step is to create a star in the center of our product. It is important to note Vedic Multiplication seems to be based on equal digit multiplication. To help account for this, students can add leading zeros as needed.

The previous step was our "middle" step. Much like Pascal's triangle there is a symmetry to our crosses and stars. For this problem we will have 1 2 3 4 3 2 1. Thus, now we will make our way back down the ladder, creating another star of three products, this time centered on the hundreds place.

Continuing down, we are again at 2, meaning we create a cross.

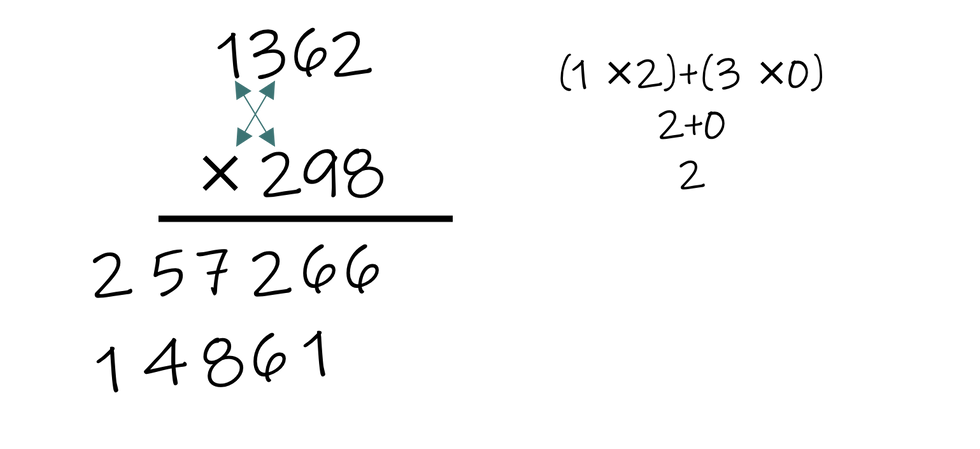
Our final step is to multiply our line straight down. In this case, as we have a 4-digit number times a 3-digit number, our value has a leading zero and thus equates to zero, leaving us only with our value to sum.

This step-by-step may have seemed overwhelming. In all fairness, we selected a more difficult example to avoid underestimating the complexity of this method. Here is a view of the line, cross, star..., cross, star with only arrows, which may help better understand the pattern present.

Vedic Multiplication Pattern

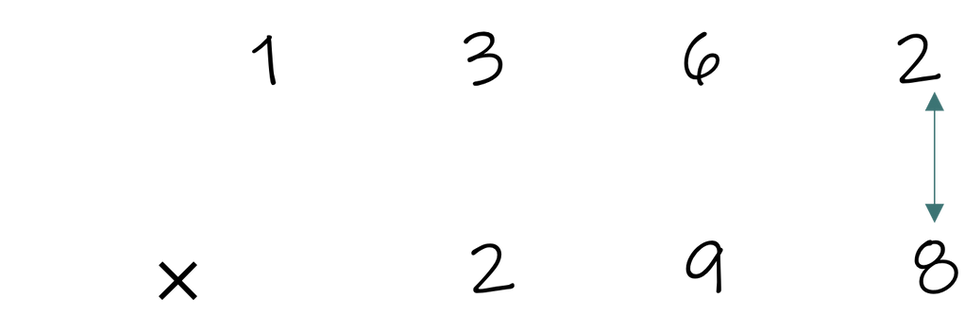
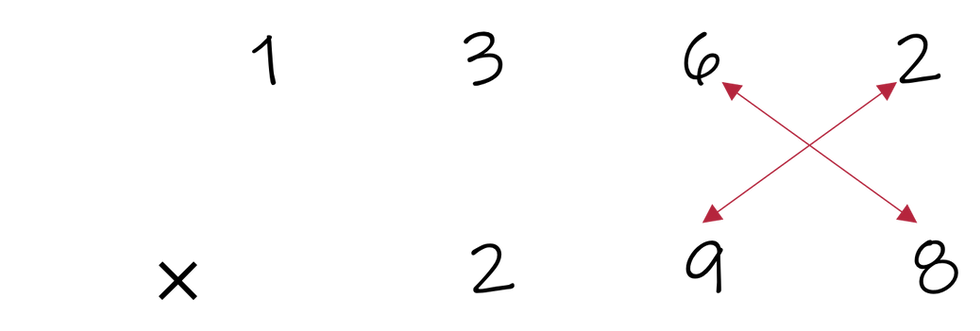
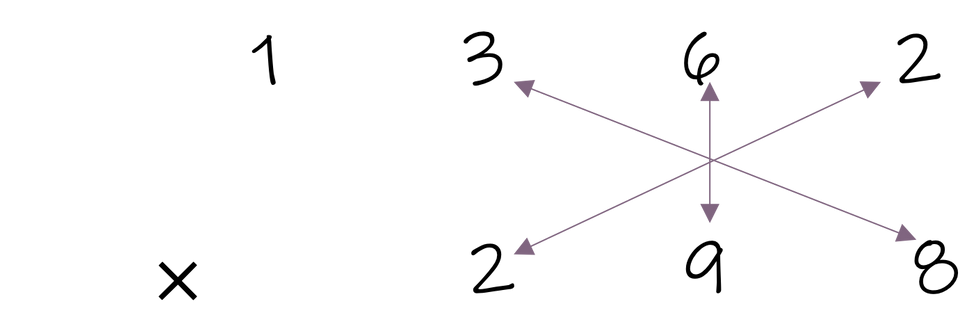
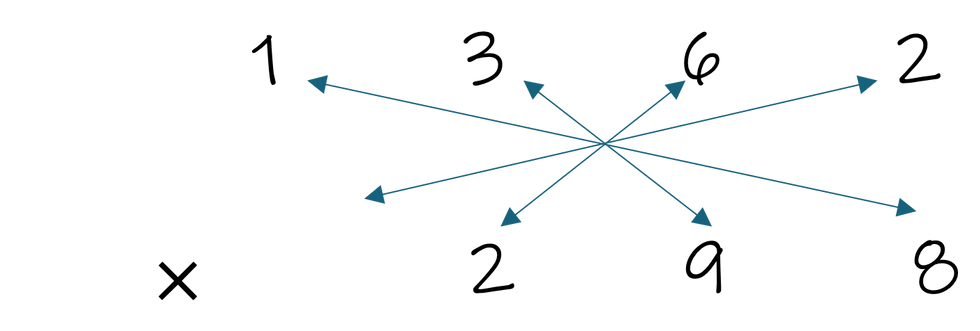
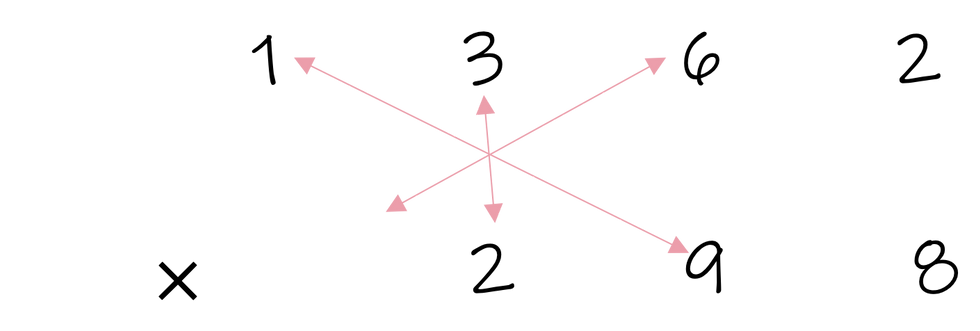
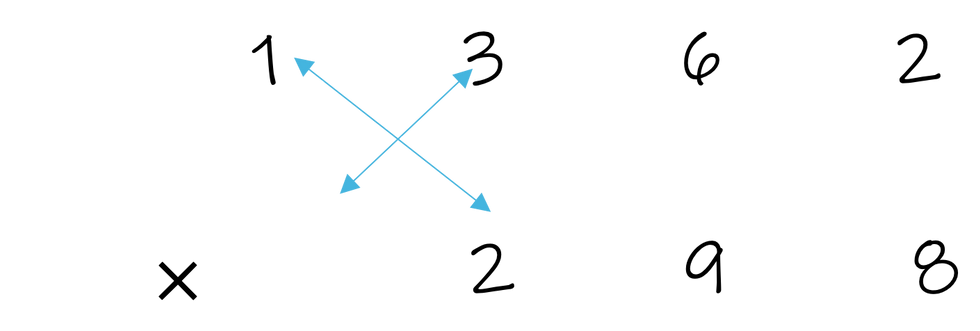
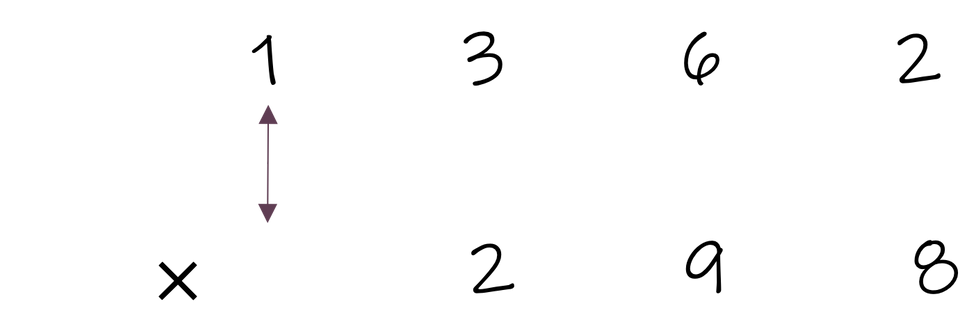
Depending on the number of digits you are multiplying, the pattern will change. Thus, this very procedural method can very easily become nonsensical to students.

Overall Assessment of Vedic Multiplication

PROS

• A beautiful result of a deep understanding of algebra

• May be easy for students with smaller values, such as 2-digit by 2-digit multiplication problems

CONS

• Very procedural

• Can easily become confusing

Our Rating:

Our Recommendation

This is really a beautiful display of a deep understanding of mathematics and algebra. Unfortunately, students learning multiplication are n where near equipped to truly understand this method. For this reason, our rating is a 2. However, when students hit Algebra 1 or Algebra 2, this is a great exercise!

In case you are interested, here is the proof we created in order to help our writers make sense of the Vedic method.

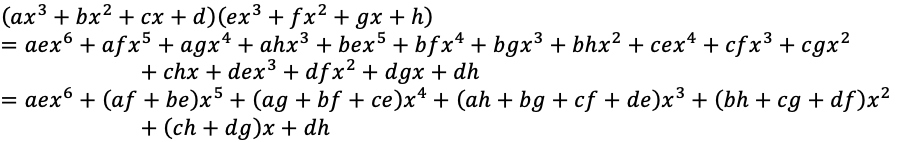
As you can see, this is much too complex for a young student to understand and it is why we recommend to skip this method.

However, this method of using algebra to help teach basics is quite in line with our MathBait™ model. The reasoning behind this is because it sets students up to already understand the basic structure of algebraic statements from a young age, making more complex topics easier to pick up by building on prior knowledge. Thus, we conclude MathBait™ Multiplication Part 4 with the MathBait™ way...