POLYNOMIALS
Polynomials are powerful formations we can find all around us. While we might jump to a curvy road, a river, or maybe a roller coaster, polynomials are used behind closed doors in almost every industry. These curves are great for modeling data. In fact, a Saint named Lagrange created a method for using polynomials to predict missing information. This is used in businesses all over the globe and can help companies make millions of dollars!
Needless to say, mastering polynomials could really pay...

Hang out with KFUN and see if you can keep up with the crew!
WHAT IS A POLYNOMIAL?
The word "poly" means many, and thus a polynomial is multiple brigades working together.
_edited.jpg)
THE TERMS
Each term includes a coefficient, a. This tells us the size of the brigade. For instance, 4x³ tells us the brigade containing three soldiers has been enlarged to four times its usual size. Note a can be any real number! We can have πx³ but we could also have 0x³.
Each term also includes a brigade. The value of n must be a whole number. A polynomial formation may not have a brigade of underground soldiers, or soldiers who have been placed in a jail cell!
Test your skills!
©MathBait created with GeoGebra
DEGREE
The degree of a polynomial is the largest brigade. Knowing this not only will help us determine a sketch of the full formation, it also tells us how many soldiers are assigned to ground zero.
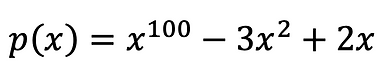
The degree of p(x) is 100!
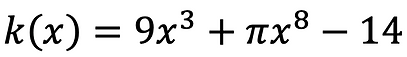
The degree of k(x) is 8!
Don't let the order trick you! You may need to reorder the terms to find the degree.
END BEHAVIOR

Knowing what is going on far-far away is super helpful in figuring out a polynomial formation. We call this end behavior. To find it, we need to think about where the formation is heading as x→∞ and as x→-∞.
The leader of a polynomial pulls the train. In many formations, soldiers with low magnitude (close to zero) simply don't have enough pull to follow their leader's commands and get in line. However, eventually, soldiers with larger magnitudes will bring things together.
This means for any polynomial, the leader will ultimately rule! While things might get a bit crazy near center stage, as we near the end of time towards positive and negative ∞, our soldiers fall into place following their leader.
Determine the degree.
Since the degree is the biggest brigade, it holds the most power. This leader will direct all the terms as they march out towards the edges of time.

Determine the behavior.
As soldiers will fall in line with their leader as they approach ±∞, to know the end behavior, we need only to look to the leader. A leader displaying an even degree will push negative soldiers to positive stations and positive soldiers to positive stations. Thus, even degree polynomials will always enter and exit the field from the same direction.
On the other hand, a leader displaying an odd degree will push negative soldiers to negative stations and positive soldiers to positive stations. Thus, odd degree polynomials will always enter the field from one direction and exit the field from the other.
An odd degree of 3 means this formation enters and exits on opposite sides of the field.
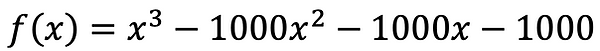

I Don't Get It
Why does an even degree mean the formation enters and exits from the same side, but an odd degree means the formation enters and exits from opposite sides?
Great question! An odd degree polynomial has a leader with a brigade of 1, 3, 5, .... What happens when we put soldiers into such a brigade?
A negative soldier, like –5, in an odd brigade always exits as a negative: (-5)³=-125. While a positive soldier in an odd brigade always exits as a positive: (5)³=125. This means polynomials with an odd degree are always moving in the opposite directions on the far left of the field for negative soldiers and the far right of the field for positive soldiers.
On the other hand, an even degree polynomial has a leader with a brigade of 2, 4, 6, .... Both negative and positive soldiers exit an even brigade as a positive because (–5)²=(5)²=25. This means polynomials with an even degree are always moving in the same direction on the far left for negative soldiers and the far right for positive soldiers.
Which way?
While even-degree polynomials will always enter and exit from the same direction and odd-degree polynomials will enter and exit from opposite directions, which way are they coming from?
This all boils down to the leading coefficient. In other words - what's the leader doing? The parents of all polynomials have a leading coefficient of 1. A negative leading coefficient means the parent has been flipped (see Transform).

This must have a positive leading coefficient like 3x²–5x+2. Notice for both negative and positive soldiers, the leader, 3x², will be positive.
3(-100)²>0 and 3(50)²>0
EVEN DEGREE
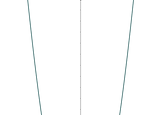

This must have a negative leading coefficient like -2x²+6x–5. Notice for both negative and positive soldiers, the leader, -2x², will be negative.
-2(-100)²<0 and -2(50)²<0
ODD DEGREE
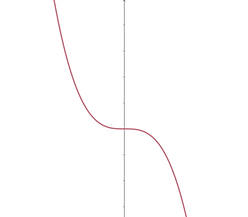
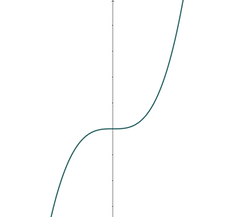
This must have a positive leading coefficient like 2x³+7x-3. Notice for negative soldiers, the leader, 2x³, will be negative: 2(-100)³<0.
But for positive soldiers, the leader will be positive: 2(75)³>0.
This must have a negative leading coefficient like -3x³-10x+1. Notice for negative soldiers, the leader, -3x³, will be positive: -3(-100)³>0.
But for positive soldiers, the leader will be negative: -3(75)³<0.

TRY IT!
As the leader will ultimately direct where the formation goes as it heads towards ±∞, we can get a good general idea of the formation's shape by simply identifying the leader. Can you climb the ranks to General by identifying where the formation is heading?
Getting every answer wrong is more challenging! If you've beaten the game, play again. This time, try to make General Three angry...
©MathBait created with GeoGebra
MULTIPLICITY
MULTIPLICITY
MULTIPLICITY
You are nearly a master of the polynomial formations! You know what is happening towards the end of time, but what is happening near center stage?
THE FUNDAMENTAL THEOREM OF ALGEBRA
The degree of a polynomial formation tells us how many soldiers are stationed on ground zero! In other words, a polynomial with degree n has exactly n roots, or anchors. This will help us to determine the overall shape.
A second degree polynomial has two soldiers assigned to ground zero like in x²-4. While a third degree polynomial has three soldiers assigned to ground zero, like in (x+3)(x-3)(x+2)=x³+2x²-9x-18. This pattern continues for any order!
All second degree polynomials have two soldiers assigned to ground zero.
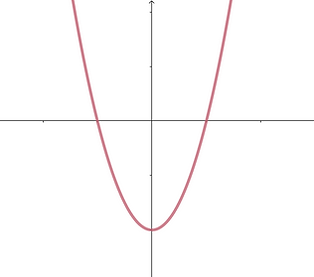
f(x)=x²-4
g(x)=x³+2x²-9x-18
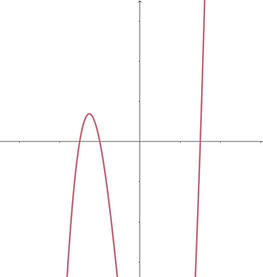
All third degree polynomials have three soldiers assigned to ground zero.
What about that?
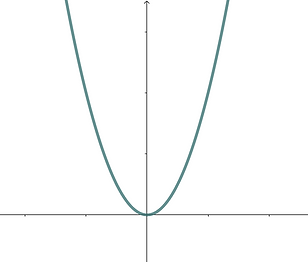
The function h(x)=x² is a second degree polynomial but looks like it only has 1 soldier at ground zero.
Excellent observation! The Fundamental Theorem of Algebra tells us a polynomial of degree n has exactly n soldiers stationed at ground zero, but it doesn't say they have to be unique! The function h(x)=x² has two soldiers at ground zero, but in this case both soldiers are x=0. The number of identical soldiers at ground zero is called multiplicity. The multiplicity of each root tells us a lot about the shape of the formation! In this case, we say the anchor x=0 has multiplicity 2.

GRAVITY
The anchors of our formation (soldiers assigned to ground zero), are pulling at the formation, keeping it grounded. Thus, the more repeated soldiers, the stronger the gravitational pull they possess. This results in a flatter formation. Go ahead and give it a try!
©MathBait created with GeoGebra
CROSS OR BOUNCE?
The area near an anchor is like a mini ecosystem of a full formation. Just as the number of soldiers assigned to ground zero tells us the degree and dictates the shape (even degrees enter and exit the field from the same direction while odd degrees enter and exit on opposite sides of the field), the number of soldiers at a specific anchor point will tell us if the formation takes on an even or odd shape at their anchor.
At x=1, the formation "crosses" ground zero. In other words, the formation enters and exits ground zero from opposite directions. Just like with a full formation, this means there must be an odd number of soldiers here!
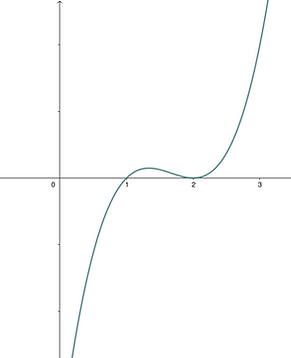
At x=2, the formation "bounces" off ground zero. In other words, the formation enters and exits ground zero from the same direction. Just like with a full formation, this means there must be an even number of soldiers here!
Why does that happen?

We don't believe in memorization either! When you understand something, it is much easier to remember and solve problems creatively. There is more than one way to make sense of crosses and bounces. Let's look at two.
I don't like to memorize. It would help if I understood why even multiplicities bounce and odd multiplicities cross the x-axis.
All polynomials can be written as the product of linear factors. Or, in other words, a polynomial is but a line times a line times a line.... This makes something special happen at ground zero.
The resulting formation sends every soldier to the product of the stations of its linear factors. For instance, since g(x) sends solider 0 to g(0)=0-1=-1 and (h(x))² sends soldier 0 to (0-2)²=4, the polynomial f(x) sends soldier 0 to (-1)(4)=-4.
We can imagine the polynomial formation f(x) as a combination of these linear orders. The first factor, g(x)=x-1, has a degree of 1, so we know it will cross. Notice how the polynomial f(x) follows the same behavior near Station 1!
Similarly, because this formation has two h(x)=x-2 factors, it forms a quadratic with an even degree. That means near x=2, the formation f(x) looks like a parabola and bounces displaying the same behavior as (x-2)².
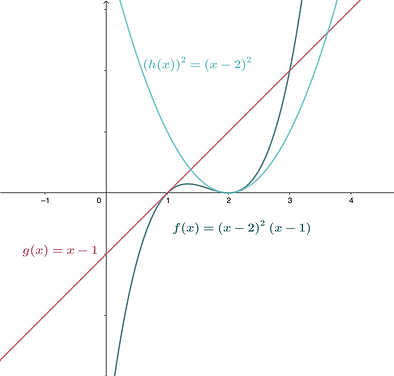
Drag the point to move across the formation and explore where each soldier is sent!
Another way to make sense of even and odd multiplicities is to consider what stations the soldiers really close to the anchors will be sent to. When you begin to explore higher math, you'll learn about limits. A limit is simply riding a formation and figuring out where the road is leading you to.
Let's take a ride on f(x)!
©MathBait created with GeoGebra
What do you notice about the soldiers right before and after an anchor point?
Q
A
Because anchor points represent the soldiers assigned to ground zero or Station Zero, all the soldiers near these anchors points are approaching Station Zero.
It's like taking a bus to Starbucks. The stops should be getting closer and closer to your destination. It wouldn't make any sense to head away from Starbucks to get to Starbucks. (Although they are everywhere so you'd probably hit one eventually anyhow).
A Case for Cases!
Let's use Penelope's cases to show why cross/bounce will work for any polynomial.
Consider some polynomial formation g(x). Let's say it has an anchor at x=k which means x-k is one of its linear factors (the lines you multiply to make g). We will let the rest of the order be h(x). For instance, in f(x) above we could let k=1 which makes
h(x)=(x-2)² as f(x)=(x-1)(x-2)². On the other hand, we could also let k=2. That would make h(x)=x-1 as f(x)=(x-2)²(x-1). In this case, n=2 as there are two soldiers assigned to the anchor at x=2.
Case 1: There is an odd number of soldiers assigned to x=k.
First consider the command c(x)=x-k.
For soldiers less than k (to the left of k) the value of x-k will be negative.
In the case of c(x)=x-1, soldiers like ½ are to the left of 1 and thus less than 1. Notice ½-1=-½. Since we are subtracting a larger number from a smaller number, the result will always be negative.
Because (x-k) is raised to an odd power, the result is negative too! For example, if we had (x-1)³, the soldiers right before 1 like ¼, ½, or even 0.9 will all be sent to negative stations from the command c(x)=x-1. Multiplying a negative an odd number of times results in another negative: (½-1)³<0.
For soldiers more than k (to the right of k) the value of x-k will be positive.
In the case of c(x)=x-1, soldiers like 1.5 are to the right and thus more than 1. This means we are subtracting a smaller value and the result will always be positive.
Now, since (x-k) is raised to an odd power, the result is positive too! Multiplying a positive number any number of times always gives us another positive.
This means the stations to the left and the right of an anchor with an odd multiplicity will always be opposite. But we've ignored the rest of the command – the h(x). Does that matter?
Yes and no. The rest of the order, h(x), simply tells us if this opposite behavior is entering Station 0 from below and exiting above, or entering from above and exiting below.
→h(x) is negative
If h(x) is negative to the left of the anchor x=k, then g(x)=(-)(-)=+. Meaning, the formation will come towards the anchor at x=k from above and cross ground zero to exit below.
→h(x) is positive
On the other hand, if h(x) is positive to the left of the anchor at x=k, g(x)=(-)(+)=-. The formation will come towards the anchor at x-k from below and cross ground zero to exit above. This is what happened in f(x) above. Because (x-2)² is positive for values close to our anchor at x=1, the formation starts below ground zero and crosses it at x=1.
Case 2: There is an even number of soldiers assigned to x=k.
Not much changes in this case. It will always be that soldiers to the left of k are smaller than k so that x-k is negative, while soldiers to the right of k are larger than k and thus x-k is positive.
Where it gets interesting is our even multiplicity. On the left, where x-k is negative, when we raise this to an even number, the result is positive! For instance, in f(x) we have (1-2)²=(-1)²=1.
But wait! On the right, where x-k is positive, we will also have a positive value when we raise a positive to an even exponent.
This means, with even multiplicities on both sides of the anchor, we have positives and thus the formation will enter and exit the anchor from the same direction.
→h(x) is negative
If h(x) is negative to the left of the anchor x=k, then g(x)=(+)(-)=-. Meaning, the formation will come towards the anchor at x=k from below and bounce off ground zero to exit below as well.
→h(x) is positive
On the other hand, if h(x) is positive to the left of the anchor at x=k, g(x)=(+)(+)=+. The formation will come towards the anchor at x-k from above and bounce off ground zero to exit above as well. This is what happened in f(x) above. Because (x-1)² is positive for values close to our anchor at x=2, the formation starts above ground zero, bounces at x=2, and exits back above ground zero too!

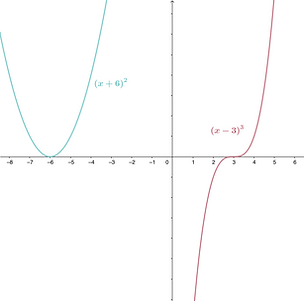
It really is just like a mini formation! The formation (x+6)² has an even degree, so we know it enters and exits the field on the same side and makes a U shape. Any formation with (x+6)² as a factor will act the same way near x=-6. Since there are an even number of -6 soldiers assigned as anchors, the formation makes a U shape and "bounces" off ground zero. Whereas (x-3)³ enters and exits on opposite sides of the field, so any polynomial formation with (x-3)³ as a factor will cross ground zero at x=3.
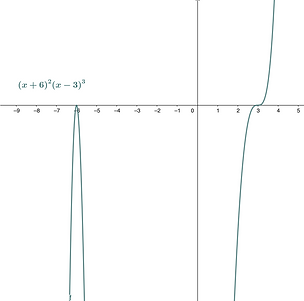
A Good Idea
DECODE
THE
CLUES
We can get a good idea of the order just by looking at a polynomial! Can you uncover the orders for these formations?
On a desktop/laptop computer hover over the formation to see the order!
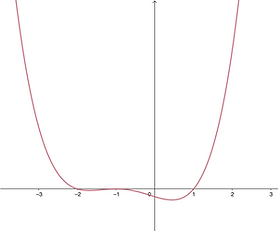
f(x)=(x+2)(x+1)²(x–1)
f(x)=(x+2)(x+1)(x–1)²
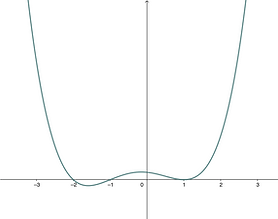
f(x)=x(x+2)²(x–1)²
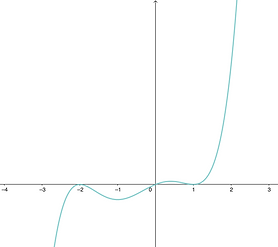
PLAY!
POLY PLAY
Think you can keep up with KFUN? It's time to hop in the backseat and test your skills with Poly Play! Listen in on the conversation and see if you can best these mathematical wizards.
How to Play
In each round you'll see a polynomial. Correctly guess the degree of the order before the members of KFUN to earn a point. One thing to be careful of is the window size. As Mr. Pikake is only drawing a part of the formation (as much that will fit on the van's window), some formations may be deceiving. But this is just for fun! If you can use the shape and the multiplicity to shout out a reasonable guess - that's huge.
This anchor is very steep! There isn't much gravity here. We might guess only 1 soldier is assigned to this post.
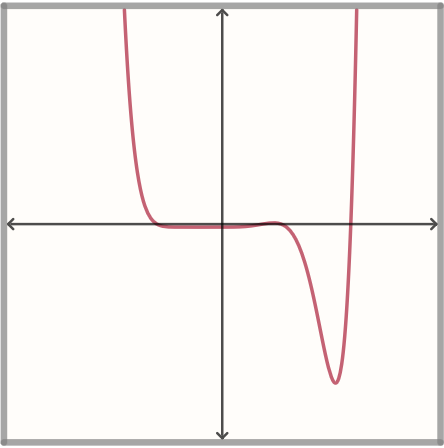
This anchor crosses, so there must be an odd number of soldiers. It is not as steep as (2). We might guess there are 3 soldiers at this location.
1
1
2
3
4
5
6
This must be an even degree as it enters and exits the field on the same side!
1
2
This anchor crosses, so there must be an odd number of soldiers. The gravity and steepness is similar to (3). We could guess there are 3 soldiers here.
3
4
This anchor is steep! It crosses, so there is an odd number of soldiers. It seems as steep as (2), so we could guess there is 1 soldier here.
5
6
This is suspicious.... The formation is dangerously close to ground zero. If we look carefully, it appears the formation changes directions. There may be a pair of soldiers at 0. Since the formation bounces, there would likely be 2 soldiers.
Good Guesses:
4, 6, 8 ,10
©MathBait created with GeoGebra




