Episode 1: Not a Math Kid & PEMDAS
- MathBait
- Jun 5, 2023
- 6 min read
Welcome to the wonderful world of Marco the Great! This is the first of twenty articles that will comprise our What’s That About? series. Each week, we will dive into a chapter of Marco the Great and the History of Numberville to provide interesting tidbits, secrets, and discussion questions to ponder as you explore the text. Put on your seatbelts and get ready for a wild ride into Numberville and beyond!
What's in this article:
Super Quick Recap
In each article, we will provide our Super Quick Recap. The goal is to give a quick overview of the chapter without any spoilers. Have other ideas? Post them in the comments!

We meet Marco.
You're ‘Not a Math Kid’ he's told.
But our story is yet to unfold.
Math is just a bunch of rules.
They seem to be made by a band of fools.
The rules keep on changing,
Marco's stuck rearranging.
What makes no sense, not even to a computer.
Now he needs a tutor...
The MATH
Chapter one takes a look at PEMDAS. The evil rule that is entirely make-believe! When we are little, we are taught to work from left to right. If we had to find 3+4–6, we’d go through the steps 3+4=7 to have 7–6 and finally arrive at the solution of 1.
As more operations are introduced, things get complicated. The internet backs us up on this one. Do a quick Facebook search for PEMDAS. You will find a concerning number of adults arguing over the result of a simple expression such as 2×1+6×6.
Why is this idea so challenging? Probably because it is made up. It has no basis in mathematics or logic and is strictly an exercise in memorization. You can use cute mnemonics like “Please Excuse My Dear Aunt Sally”, but like most memorization techniques this is likely to result in more troubles.
After all, if we follow this mnemonic directly, the solution to 6÷3×4 would be ½ (since it tells us ‘My’ comes before ‘Dear’, we multiply and then divide). Any math teacher would tell you the solution is actually 8. Wait… what?
Yep. It isn’t enough to memorize PEMDAS, you have to understand it too. We made this nifty visual to help you out.
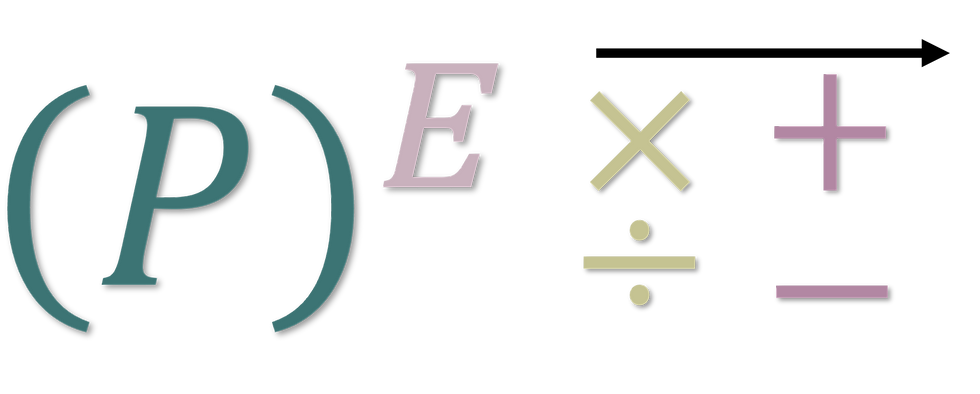
Here, we can see how things work a little better. We start with the Parentheses (), completing anything inside first. Then we move to Exponents, the little terrifying baby numbers that sit on a shoulder like a pirate’s pet parrot. Now things get trickier. It isn’t really MD as in multiplication then division. It turns out (as you will later learn in Marco the Great) that multiplication and division are the SAME THING! We know, it’s mind blowing. Because they are equivalent operations, next you work from left to right doing whichever of these operations you come across first. This is why 6÷3×4=8. We don’t actually perform the multiplication first; we complete division and multiplication as it comes from left to right.
You can probably foresee what’s next. Subtraction and addition are also the SAME THING! We wrap things up by moving from left to right, tackling any Addition or Subtraction that crosses our path.
What is interesting about PEMDAS is that it was created as a way for us all to understand any math expression in the same way. When someone points to the sky and says, “look at that bird”, we all know what to look for. We ignore the planes and the clouds and the UFOs and search for the winged living thing instead. That’s because we all have an agreed upon understanding of the meaning of the word “bird”.
Math expressions are statements in the same way. If someone tells us 6÷3×4, we need to understand if they are trying to tell us ‘8’ or ‘½’. Hence, PEMDAS was born. Because it is made up, not intuitive, and not based in any understanding (in fact, we introduce PEMDAS before students even have any understanding that addition & subtraction are the same operation so the idea that the two ‘hold the same weight’ is challenging to grasp) it is no wonder lots of students (and adults!) have trouble with it.
To make matters even worse, students then go on to learn new methods and properties that blow PEMDAS out of the water. If we saw something like 4 × (10+3) we don’t actually need to compute the parentheses first. Thanks to the Distributive Property (or as the Numberfolk see it, the evil wizard) we can compute the multiplication first and obliterate the parentheses entirely.
Thus, if your kiddo is confused with Order of Operations, don’t blame them. It is confusing. In fact, it’s a bit nonsensical. At MathBait we help students to make sense of these tricky concepts rather than memorizing rules. In our online game Monster Dialects students see how math expressions are just like a language as they translate alien phrases. This, along with discussing why multiplication and division or addition and subtraction are equivalent operations, and hence hold the same weight, allows them to develop a strong foundation in decoding mathematical expressions that will last them well into their college years.
The QUOTE
“Somehow it’s okay for people to chuckle about not being good at math. Yet, if I said, ‘I never learned to read’ they’d say I was an illiterate dolt.”
-Neil deGrasse Tyson
In Chapter 1, Marco’s teacher announces he is ‘not a math kid’, a phrase that allows him to get away with subpar performance in class. Unfortunately, this happens every day. We see it from teachers and parents posting phrases like “my kid isn’t very mathy”.
What we love about deGrasse Tyson’s quote is that it brings to light how silly this idea is. Somehow as a society we have made it okay to sort our children into groups that predetermine their capabilities in mathematics, yet we don’t have the same titles in other subjects.
In fact, there is no such thing as a ‘math kid’ and thus it is impossible to ‘not’ be one. The real problem is how mathematics is presented. This is precisely why we picked Order of Operations for this chapter. There are plenty of things we teach students in the early grades that are bound to cause cognitive dissonance later on. Some students may have less of a struggle working through this confusion than others but that doesn’t mean they are more mathematically capable.
We can think of understanding like a code. There are lots of coding languages – C++, Java, FORTRAN, Visual Basic, the list goes on. Each and every one of these languages is in fact capable of the same thing. However, getting the program to do the command you want looks different and is harder/easier depending on the language your working in.
If you think you have a kid that is ‘not mathy’ try using a different code. Each and every student is capable of not only understanding but flourishing in mathematics given the right approach. With Marco the Great and the History of Numberville we use analogies to help all students develop a mastery of the ideas addressed. Why analogies? Well, you’ll have to subscribe to our What’s That About? series to find out! We will be discussing this in depth in an upcoming article. The key idea is the same: every kid is a math kid once you figure out the coding language they function in.
Each and every student is capable of not only understanding but flourishing in mathematics given the right approach.
Discussion Questions
Reading Marco the Great and the History of Numberville with your children or students? Here are some discussion questions to get you thinking and talking.
Reading Questions
Marco feels like Maggie gets special treatment since she is Peter’s biological daughter. How do you think Maggie feels?
If someone told you it was okay to not do well in a class, what would you do? Even though Marco has a ‘not a math kid’ badge, he doesn’t like feeling lost and falling behind his peers. Would you feel the same or differently?
Why do you think people sometimes say kids are ‘not math kids’ but they don’t say they are ‘not history kids’?
Math Questions
There are 8 math rules Marco memorized in Chapter 1. Which rules contradict each other?
Can you rewrite Marco’s rules so they make sense together?
How could Marco’s teacher present the rules in a way that they would make more sense. (For instance, maybe if rather than teach the class to always go from left to right, could Mrs. Sanders say this in a way that makes it easier for students when it is time to understand PEMDAS?)
Stay tuned to learn more about Marco the Great and the History of Numberville with our weekly series What’s That About?
Interested in some humorous PEMDAS gear that is sure to strike up a conversation? Visit our shop!







Comments