An Optical Illusion or a Critical Mathematical Error? The Curry Paradox
- MathBait

- Mar 8, 2023
- 6 min read
Updated: Mar 30, 2023

On World Math(s) Day we posted an interesting puzzle that got lost in our twelve (yes twelve - one each hour in celebration) posts that day.
A mix of psychology, optical illusion, and mathematics, this puzzle is an important one and a great discussion starter for all levels of student.
In this article, we will explore our Paradox Puzzle, reveal the trick, and explain why it is so important for any budding mathematician!
The Puzzle
Before we dive into the magic of this amazing paradox, take 30 seconds to view the clip to get up to speed.
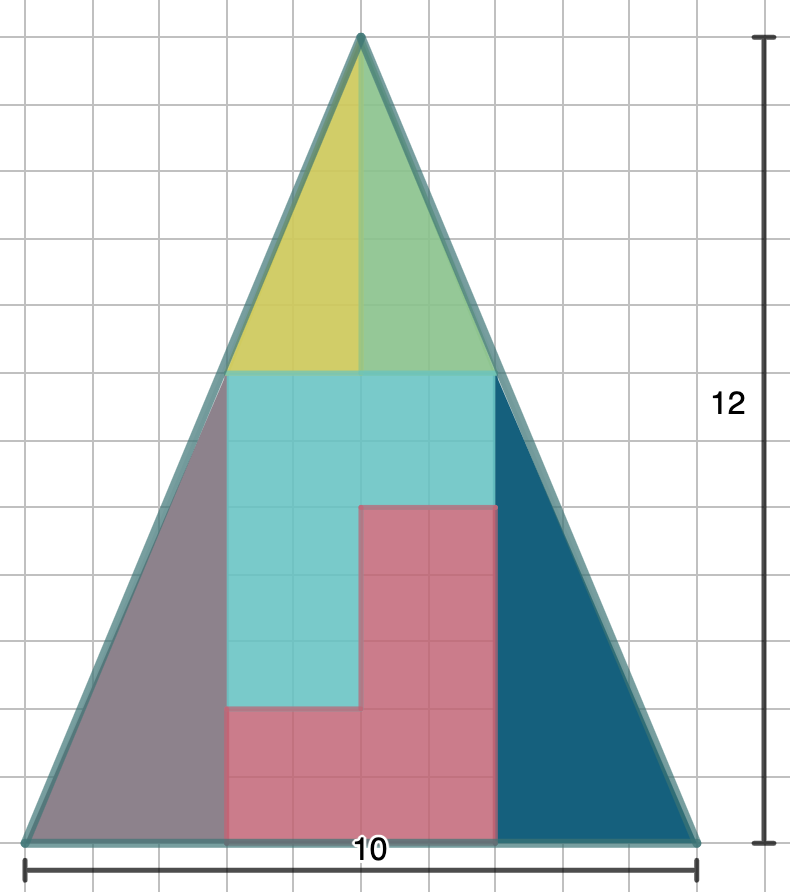
What's happening here? We begin with a simple triangle. Puzzle pieces have been arranged to fit snuggly within its sides. No gaps or holes are present. Using our geometry knowledge, we can figure out that together the puzzle pieces have an area of ½(10)(12)=60.
Next, we are taken through series of animations that shows viewers a new solution to the puzzle. After creating a duplicate of the triangle, each piece goes through a series of isometric transformations.
What's an Isometry?
An isometric transformation is a flip, spin, or slide (also known as reflections, rotations, and translations) that don't change the basic structure of the shape. Just like a normal puzzle, you can move the pieces around, slide them across the table, and the piece doesn't change as long as you don't accidentally bend or rip it. Isometries map the original (called the pre-image) to a new congruent figure that is the same size and shape (just called the image).
This is important because it means moving the pieces hasn't changed their properties. An example of a non-isometric transformation is a dilation. Zoom in on the screen. Inherently, nothing has changed. However, the size of the images and text has been transformed. If you took a screenshot of the zoomed in triangle and one of the original, they would not fit perfectly atop each other. This means the original and the new image are similar but not congruent.
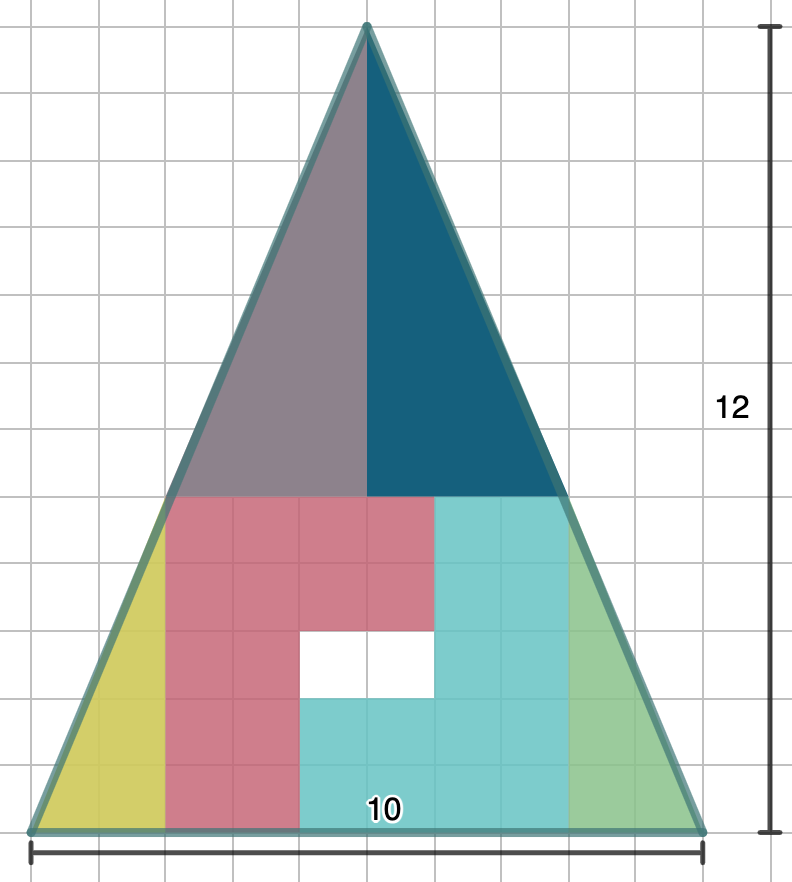
If our movement didn't change the size or shape of the pieces, or the triangle, how is it possible we have a big hole in our new image? This is telling us that the area of the puzzle pieces is ½(10)(12)-2=58! In this simple and deceiving little puzzle we have shown that 60=58. That can't be possible... can it?
We have shown 60=58!
What is going on with the strange and fascinating triangle? Let's dive into the 'trick' that is deceiving us.
The Trick
Mathematically, the 'trick' is very hard to discern from the images. If we take a closer look, we can see that the slope, the incline, of the left side of the triangle is 12/5. You can find this by calculating from the bottom-left vertex to the top vertex how many steps up we take and divide that by how many steps to the right we take.
Now take a look at the smaller yellow triangle. It appears to have a slope of 5/2. And the triangle on the top left of the figure appears to have a slope of 7/3. If you average these two slopes you get approximately 2.41666... very close to the slope of the large triangle which is 12/5=2.4!
Normally, we ignore a small discrepancy like this. We round 2.41666... to 2.4 and call it a day. We don't think anything of it. In this case, doing so allowed us to show 60=58! It turns out all those decimal places are important, really important, and can have a huge impact on what we are trying to find.
Paul Curry, a magician, created this puzzle in 1953. It is a perfect sleight of hand trick to make the impossible possible! But as it turns out, it is just math, some really important math that most of us ignore that can make a huge difference.
The Important Math Lesson
While Curry's paradox is certainly interesting, it is at its heart an optical illusion. A trick of our sight rather than of mathematics. So why is this puzzle interesting to mathematicians? Error!
In school, students mostly solve 'nice' problems with 'nice' solutions. In the real world, problems are rarely nice. Most applications involve some sort of measurement. There is a good reason for the old saying 'measure twice, cut once'; measurements are notoriously inaccurate. This means every time mathematicians measure something, it comes with a margin of error. You might have heard this called Significant Figures. The number of significant figures is the amount of error we are willing to accept.

But just because we are willing to accept some error, that doesn't mean we always get what we expect! For this project, a student built a truncated dodecahedron. They reported they designed the polyhedron such that each side was constructed to be 2 cm. Their next task was to determine the surface area of the 20 equilateral triangles.
They measured their materials (twice, cut once) and found the triangles to have a height of about 1.7cm. This sounds like a reasonable amount. It is pretty hard to measure much more precisely with centimeters.
Putting their information together, each triangle would have an area of ½(2)(1.7) cm² simplified to 1.7 cm². Since there are 20 of these all together, we calculate 20(1.7) to arrive at a total surface area of equilateral triangles measuring 34 cm².
Everything looks good here. What's the problem? Error. The height of an equilateral triangle with sides measuring 2 units is √3. While this is very close to 1.7, it is not 1.7. When we multiply, we compound the area. The real surface area? 20√3 cm². This is an exact number with no error at all! We normally don't need to be totally exact in the real world (how am I supposed to cut to equal exactly √3?), so if we wait to round until all our calculations are finished we get 35 cm². We find we were a full square centimeter off!
While this example is small potatoes, rounding and compounding error can put us significantly off from a good estimation. In fact, it is one of the most fatal errors a mathematician can make. When we are pretty close (like in our Curry Triangle), so much so that the difference seems negligible, we tend to ignore it. Throw it out with the trash. The problem is, those tiny pieces can add up to be big!

We will leave you with one last example. This one, you probably have heard of before. It focuses on your money. Say you place your $100 birthday check in a savings account that boasts 6.796% interest. If that is a yearly interest then after one year, if you left the entire amount in the bank, you would earn (100)(6.796%) in interest. That computes to $6.796 your money earned. Cool! But wait, there isn't such a thing as 79.6 cents. I can have 79 cents or 80 cents, but I can't have 79.6 cents
What happens to that extra decimal place? Banks certainly don't want to give you more than you earned, so 6.796 is likely to show up in your account as $6.79. Where did the $0.006 go? A very smart young man once asked that exact question. He then diverted these fractions of a penny, amounts that no one would miss, to his own account. The result? He became a millionaire! The fractions of a cent compounded and when coming in from many many accounts, what once appeared negligible turned into something very profitable!
The Morale of the Story
The Curry Triangles are a fun puzzle to present to students of all ages. They allow us to seemingly show something impossible (that 58=60). And while it is an interesting tangent, it ties nicely into the key mathematical concept of error. When we round, we are losing important information. Sometimes that is okay. We understand there is some small amount of error in our calculations and call that negligible. We can go to sleep at night knowing we left off a few trailing digits. But Beware! Those tiny amounts can come together, form a formidable army that is much stronger and mightier than any individual solider! And when our error is compounded the world no longer makes sense. It is a strange place where 58 and 60 are the same, fractions of a penny turn to millions of dollars, and a simple change of viewpoint reveals a gaping hole that once was not there.
So remember, measure twice cut once and keep things exact for as long as you can! Only round at the very end otherwise what seems like nothing will leave you miles from where you expected to be.





Comments